The Psychology of Quality and More
|
The Psychology of Quality and More |
Histograms part 1: creating themQuality Tools > Tools of the Trade > 64: Histograms part 1: creating them
When measuring a process, it often occurs that the measurements vary within a range of values. Thus, for example, in manufacturing resistors, 220 ohm resistors will not all be exactly 220 ohms, but will vary in value around 220 ohms. By understanding how these measurements vary, the effects of the process and changes made to it can be better understood. The Histogram is a specific form of bar chart that shows a frequency distribution across a set of measurements. The width of each bar is constant and represents a fixed range of measurements (called a cell, bin or class). The height of each bar is proportional to the number of measurements within that cell. Each bar gives a solid visual impression of the number of measurements in it and together the bars show the distribution across the measurement range. This visual shape is far easier to interpret than a table of numbers, as in the diagram below.
Fig. 1. Histogram
is easier to understand than a list of measures In drawing the Histogram, there must be a sufficient number of measurements to be able to give a usable shape to the distribution. The number and width of the bars are also important; if the bars are too narrow, then insufficient measurements will fall into each bar to give it significant height. Similarly, if the bars are too wide, there will be too few bars to give a useful shape to the distribution. Width of each barTo enable enough bars to be drawn, a large number of measures are needed – typically 100 or more. If you use less, then the natural shape of the curve will become increasingly hidden in a ragged outline. To compensate for this, you can use the following table to help decide on the number of bars to show. Table 1. Deciding
on the number of bars
An alternative method is to use the Number of bars = 1 +
3.3 * log10 (number
of measurements)
|
|
Bar number |
Measure from |
Measure to |
Total of measures |
|
1 |
10.0 |
14.9 |
1 |
|
2 |
15.0 |
19.9 |
6 |
|
3 |
20.0 |
24.9 |
15 |
|
4 |
25.0 |
29.9 |
32 |
|
5 |
30.0 |
34.9 |
35 |
|
6 |
35.0 |
39.9 |
12 |
|
7 |
40.0 |
44.9 |
7 |
|
8 |
45.0 |
49.9 |
2 |
It is now a simple step to draw the Histogram from the table. If you are using something like Microsoft Excel, it is a snap to select the final column and click on the graph button.
A useful variation on the Histogram is the ‘Stem and Leaf plot’, as below. Here, rather than have a blank bar, the additional information about the fractional part of each measurement is shown in the bar. Thus the central bar is made up of two measures of 4.5, one measure of 4.6, three measures of 4.7 and one of 4.9. This gives a second level of information, for example showing the mode (the most common value) of the middle bar to be 4.7.
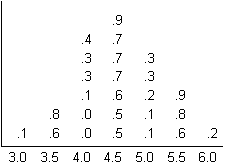
Fig. 2. Stem and
Leaf plot
Next time:
Histograms
(part 2: interpreting them)
This article first appeared in Quality World, the journal of the Institute for Quality Assurance
Site Menu |
|
Quality: | Quality Toolbook | Tools of the Trade | Improvement Encyclopedia | Quality Articles | Being Creative | Being Persuasive | |
|
And: | C Style (Book) | Stories | Articles | Bookstore | My Photos | About | Contact | |
|
Settings: | Computer layout | Mobile layout | Small font | Medium font | Large font | Translate | |
You can buy books here |
|
And the big |